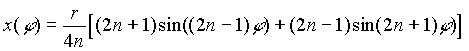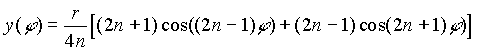Vortrag auf der DPG-Tagung des Fachauschusses ‘Didaktik der Physik’ am 10.3.1997 in Berlin |
||||||||||||||||||||||||||
Der Kaustikeffekt tritt auch sehr gut in einem zylindrischen, innen polierten Ehering auf. Um diese Erscheinungen noch besser reproduzieren zu können, habe ich einen Messingring von etwa 4cm Durchmesser innen poliert. Mit einer kleinen Halogen-Lampe lassen sich die Kaustiken hervorragend erzeugen. Damit sind auch die Fotos in Abb. 20 erstellt.
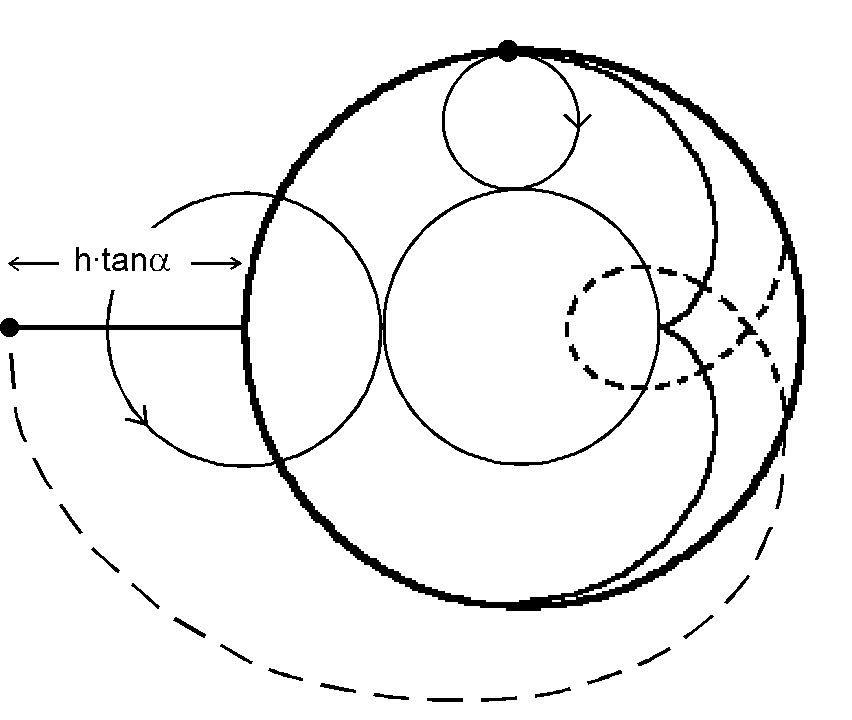
Kaustiken sind von der Optik her bei sphärischen Linsen und Hohlspiegeln schon lange bekannt. Bereits Christian Huyghens (1629-1695) hat sie beschrieben. Der Schweizer Mathematiker Johann Bernoulli (1667-1748) hat die formelmäßige Beschreibung als sogenannte Epizykloide veröffentlicht [9]. Eine Epizykloide entsteht durch Abrollen eines Kreises auf einem anderen Kreis. Der Fall ganz rechts aus Abb. 20 sei beispielhaft herausgegriffen. In Abb. 21 sind die beobachtbaren Strukturen herausgezeichnet. Einerseits die klassische Kaustik, andererseits die überlagerte Schleife. Sei r der Innenradius des Zylinders, dann entsteht der Rand der klassischen Kaustik durch Abrollen eines Kreises mit r/4 auf einem zentralen Kreis mit r/2. Der kleine r/4-Kreis ist oberhalb des r/2-Kreises dargestellt. Der Rand der Schleife hingegen wird durch Abrollen eines r/2-Kreises auf dem zentralen r/2-Kreis bewirkt, wobei aber der die Zykloide erzeugende Punkt sich im Abstand h·tan a vom Mittelpunkt des Kreises auf der Verlängerung des Radius befindet. Man spricht in diesem Fall auch von einer verlängerten Epizykloide.
Die parametrische Darstellung der hier entstehenden Kaustiken lautet [10]:
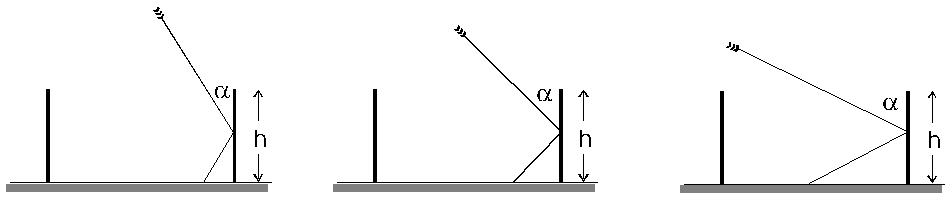
Man kann sich die Frage stellen, wie sich die Kaustik verändert, wenn der Einfallswinkel a immer größer wird. In Abb. 23 ist das schematisch und mit den entsprechenden Fotos darunter wiedergegeben. Je größer der Winkel a , d.h. je flacher das Licht in den Ring einfällt, um so mehr Reflexionen im Ring sind möglich. Bei zwei Reflexionen ergibt sich eine herzförmige Figur. Bei drei Reflexionen ebenfalls. Je mehr Reflexionen, um so kleiner und schwächer wird das Herz, aber es bleibt ein Herz. Etwa ab der fünften oder sechsten Mehrfachreflexion läßt sich die Erscheinung praktisch nicht mehr beobachten, da sie zu lichtschwach wird.
Auch hier sind die so entstehenden Kaustiken mit einer parametrischen Darstellung von Epizykloiden zu beschreiben, wobei die Anzahl der Reflexionen durch den Parameter n charakterisiert wird [11]:
Die mathematischen Darstellungen der im vorhergehenden beschriebenen Kaustiken hat der Physikstudent C. Engelhardt erarbeitet. Natürlich erhebt sich die Frage, ob das nicht längst schon irgendwo publiziert ist. Das ist tatsächlich so. Aber es ist nicht leicht zu finden, da die entsprechende, ziemlich mühsam zu lesende Veröffentlichung aus dem Jahre 1852 stammt [12]. C. Engelhardt war dennoch nicht frustriert. Einerseits hat er sich von einer elementaren physikalischen Beobachtung selbstständig bis zur mathematischen Formulierung vorangearbeitet. Zum anderen hat er weitergehende Beobachtungen und Überlegungen angestellt, die möglicherweise noch in eine Publikation bzw. Diplomarbeit in Mathematik für ihn münden. |
||||||||||||||||||||||||||
| [Start-Seite] [Seite vor] [Seite zurück] |
||||||||||||||||||||||||||